Liu Hui's derivation for the volume of pyramids (with a photo of a Zometool model!)
Liu Hui 劉徽 (ca. 263 AD) was a mathematician from the Wei Empire (魏國) in modern-day Northern China. His most important contribution was his commentary on the Nine Chapters of Mathematical Art (九章算術). One of the most interesting pieces of his commentary is his demonstration of the volume formulae of two kinds of pyramids: yangma 陽馬 and bienao 鼈臑.
The pyramid on the left of the figure below is a yangma, and the one on the right is a bienao. In modern mathematics, we need to use calculus to prove their volume formulae, which are 1/3 of length by width by height and 1/6 of length by width by height, respectively.
 Liu Hui's demonstration also involves an infinite process. The method of Liu Hui's way of continued division is shown by the figure and also the photo of a model made from Zometool
Liu Hui's demonstration also involves an infinite process. The method of Liu Hui's way of continued division is shown by the figure and also the photo of a model made from Zometool
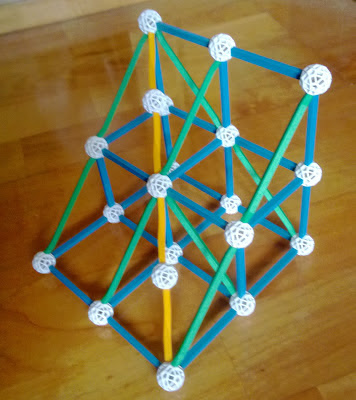
Following is a sketch
of Liu Hui’s argument rendered with the help of modern symbolism and terminology.
Before the procedures for these two pyramids, Liu had already shown in the commentary that the volume of a qiandu (壍堵, a triangular prism) is half of that of a cuboid with
the same dimensions. Suppose that the yangma
and the bienao in question have
dimensions l, w and h. They can be
fitted together to form a qiandu with
the same dimensions. Liu then sets out to demonstrate that the volume of the yangma is twice that of the bienao. As can be seen in the Figure, the yangma can be divided into one cuboid,
two qiandu and two smaller yangma, all of whose dimensions are l/2, w/2
and h/2, and the bienao can be divided into two qiandu
and two smaller bienao, all of whose
dimensions are also l/2, w/2 and h/2. Comparing the one cuboid and the two qiandu obtained from the yangma,
and the two qiandu obtained from the bienao, he argues that the sum of the volumes
of the former is twice the sum of the volumes of the latter, since the volume
of a qiandu is half of that of a
cuboid with the same dimensions. Now he is left with two smaller yangma and two smaller bienao. Since the dimensions of each
smaller yangma are half of those of
the original yangma, the volume of
the smaller is one eighth of that of the original. Thus the total volume of the
two smaller yangma is a quarter of that
of the original yangma. Similarly,
the total volume of the two smaller bienao
is a quarter of that of the original bienao.
Next, he can divide the smaller yangma
and bienao in the same way as in the
previous step and then continue. In the nth
step he would obtain 2n
- 1 cuboids, 2n qiandu and 2n smaller yangma
from the yangma in the previous step,
and he would obtain 2n qiandu and 2n smaller bienao
from the bienao in the previous step.
Similar to the first step, the sum of the volumes of the 2n – 1 cuboids and 2n qiandu from
the yangma is twice that of the 2n qiandu from the bienao. He
then argues that the smaller yangma
and bienao that are cut out in each
step get finer and finer until they eventually become “without form” (無形), so he only needs
to consider the cuboids and qiandu
that are cut out in each step in determining the volume. Since in every step
the sum of the volumes of the cuboids and qiandu
from the yangma is twice that of the qiandu from the bienao, Liu Hui concludes that the volume of a yangma is twice that of a bienao.
Since the yangma and the bienao can be fitted together to form a qiandu, whose volume is lwh/2, it follows that the volumes of
the yangma and the bienao are lwh/3 and lwh/6,
respectively.
Reference


No comments:
Post a Comment